Hashtable (tabela de dispersão)

A hashtable é uma implementação do dicionário, que por meio de uma função de dispersão consegue dispôr os elementos na lista de forma “aleatória”, mantendo a complexidade temporal da pesquisa em O(1).

A ideia é que, usando um array, a função de dispersão defina a posição do elemento sendo inserido. Como essa posição é calculada em (O(1)), a pesquisa usando a mesma chave vai chamar a função de dispersão e acessar direto o endereço do elemento no array, em tempo constante.

1. A função de dispersão

A função de dispersão precisa levar em conta o tamanho do array, caso contrário ela pode usar somente parte do array (o que levaria a mais colisões) ou fazer inserções em endereços que estão fora da área de memória.

Uma função de dispersão comum seria h(x) = x%tamanhoDoArray.

2. Inserção

Considere um array de tamanho 12:

Vamos inserir alguns números. 23, 178, 38 e 56. Ficamos assim:

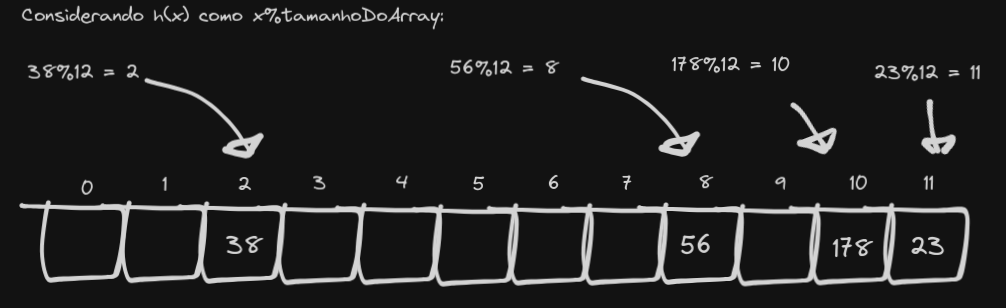
Como a posição do número no array vai depender do resto da divisão dele por 12, você pode esperar que haja uma distribuição uniforme ao longo do array.

Mas vez ou outra o resultado da função hash pra um elemento vai ser uma posição que já está ocupada, e temos que resolver isso de alguma forma.

3. Lidando com colisões

Vamos pegar o exemplo do item 2 e adicionar o número 14.

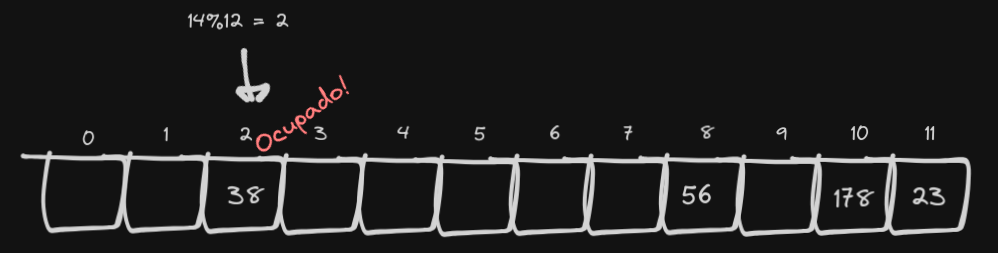
Ooops, ocupado. Há duas formas mais comuns de lidar com colisões:

3.1 Encadeamento

Uma forma simples de resolver o problema das colisões é armazenar os itens numa sequência (lista, array). Você pode desde o início usar um array de listas ligadas, por exemplo. No meu caso, eu criei um objeto “Elemento” que vai armazenar o valor do elemento e uma referência para o próximo elemento naquele endereço, caso haja um.

Vejamos:

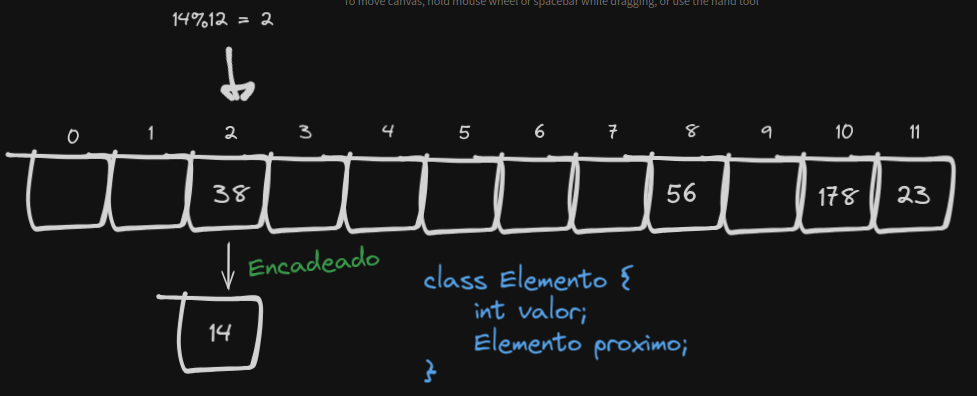
Dessa forma, nosso algoritmo de pesquisa vai precisar iterar sobre todos os elementos ligados ao primeiro do índice, para conferir se o item buscado não está lá.

3.2 Endereçamento

Endereçamento é um método onde arranjamos o elemento em outra posição no array, e pode ser feito tradicionalmente de duas formas:

3.2.1 Linear probing

Linear probing consiste em deslocar o elemento para o índice seguinte. Retomando o exemplo da imagem do item 3:

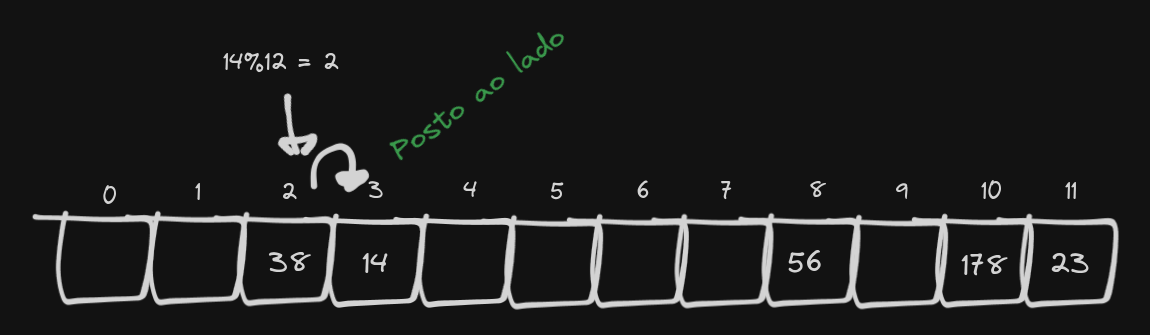
E então nossa busca precisa passar por todos os espaços preenchidos até achar um elemento vazio.

Mas há um problema aí. Vamos considerar o seguinte: Inserimos o número 26 na tabela, que também depois da função de hashing acaba caindo no índice 2. Depois, por algum motivo, removemos o elemento 14.

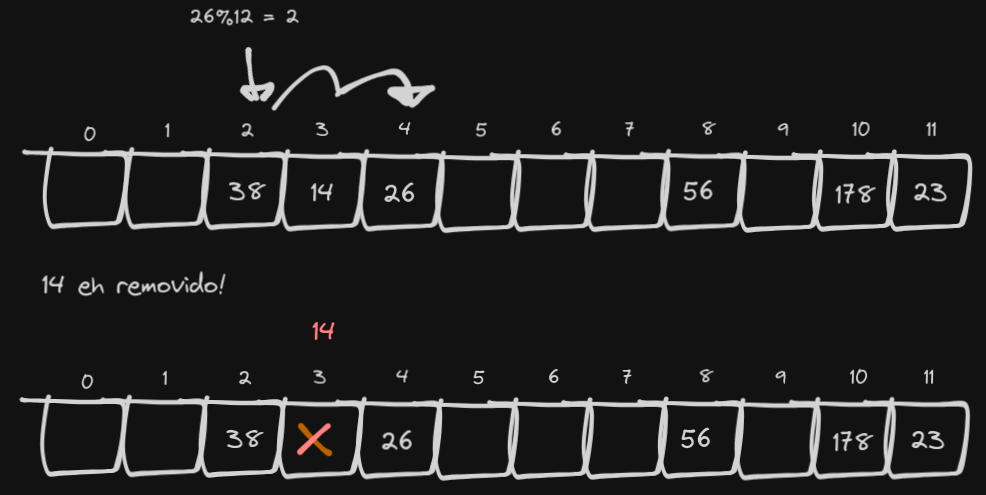
Até aí tudo bem, NÉ?. Mas vamos fazer uma pesquisa pelo número 26:

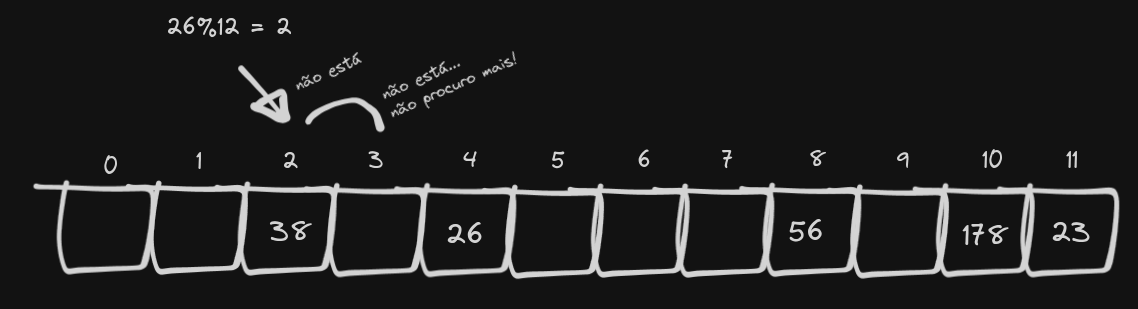
O “buraco” que deixamos ao remover o número 14 faz com que não consigamos chegar no 26, que foi posto na “mesma posição” mas que agora não pode ser acessado. Você pode até dizer que é só procurarmos no resto do array, mas isso torna a complexidade temporal da busca O(N), fazendo com que nossa implementação vire basicamente uma lista ligada:

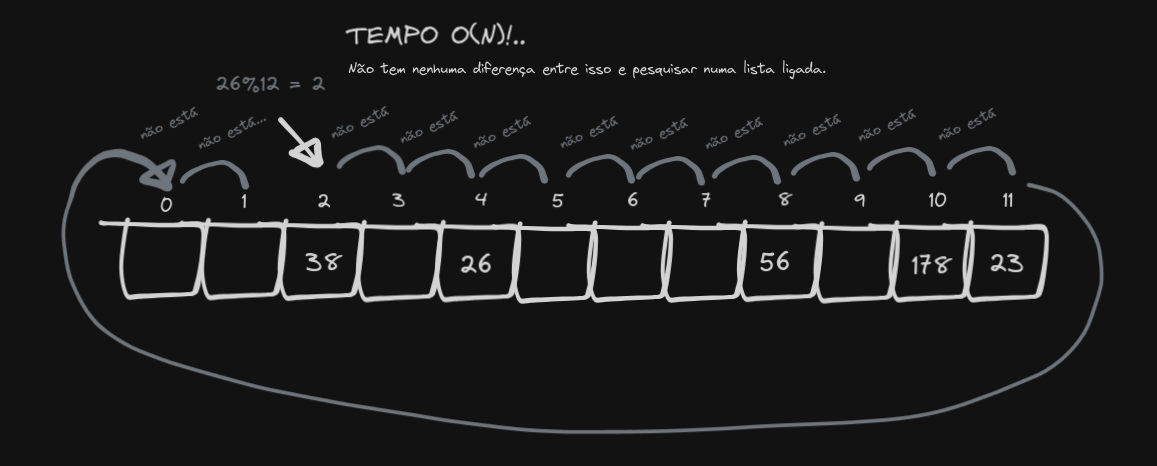
A solução pra o problema do buraco é, quando fizermos uma remoção, utilizarmos um símbolo, que indica que ali é um espaço vazio, mas que o próximo elemento deve ser conferido também. Coleguinha chama esse símbolo de “AVAILABLE”.

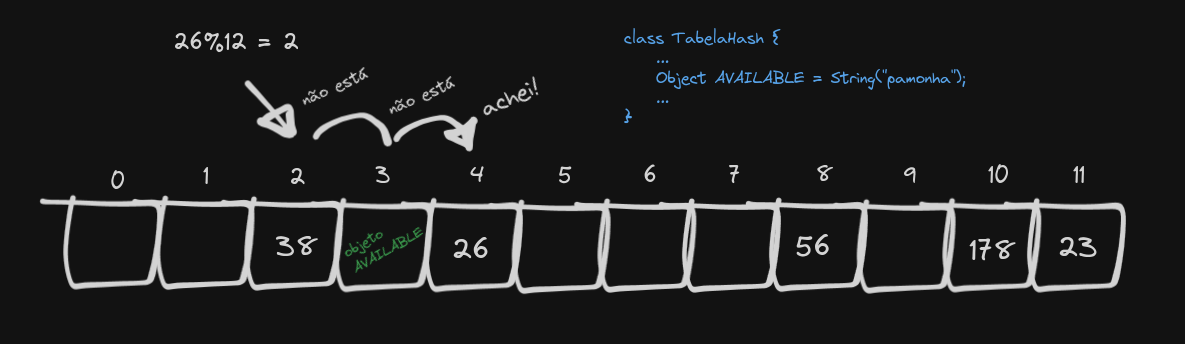
Ufa! Temos uma tabela hash com linear probing funcional. O objeto AVAILABLE simboliza que aquele índice pode ser passado numa pesquisa, mas que também está disponível (no inglês, available) para inserção.

Porém, eu não gosto dessa abordagem. Pra usar ela, o tipo do atributo que usamos como chave para nossos valores na table precisa ser Object, e isso não é tão limpo: generalizar o tipo de todo um conjunto pra satisfazer uma condição excepcional.

…….. COMO EU AINDA NÃO CITEI TAMANHO MÁXIMO DO ARRAY, É BOM DEIXAR ESSA PARTE PRA MAIS PRA FRENTE.

…..TAMBÉ LEMBRAR DE CITAR QUE É NECESSÁRIO CHECAR O ELEMENTO DO INDÍCE ATUAL CONTRA O SIMBOLO AVAILABLE.

Acho mais interesante usarmos a seguinte opção: O nosso “available” será um número que não poderemos usar. O ideal pra isso é o número máximo que o tipo do atributo da chave suportar. Como uso int, nosso símbolo de available será o número 2 147 483 647. Em java, podemos acessar esse valor por meio de

Integer.MAX_VALUE

Logo, nosso exemplo ficaria assim:

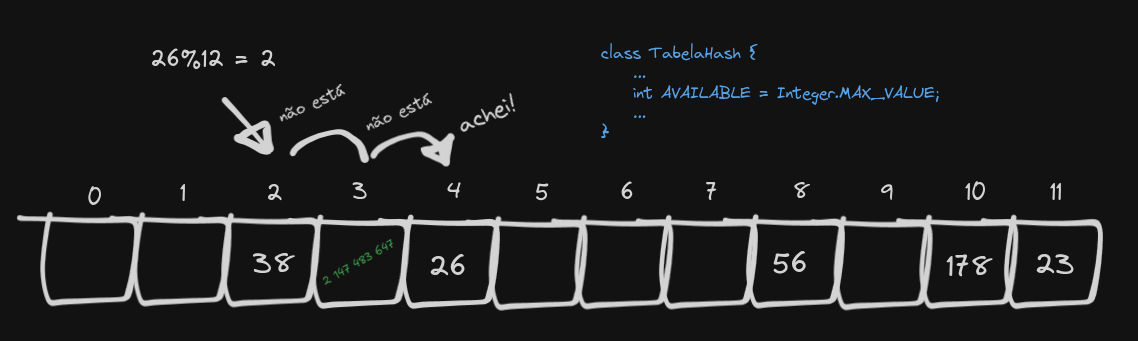
Vamos adicionar mais alguns elementos:

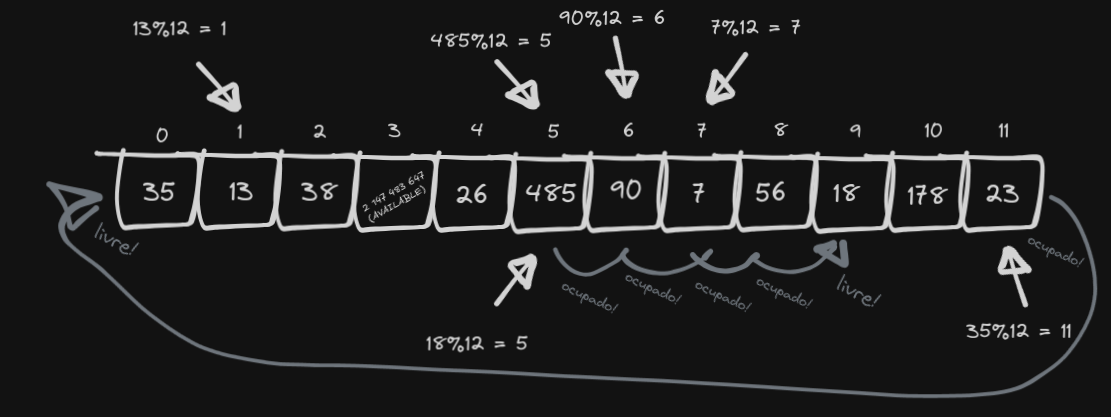
Note que a tabela é circular.

Talvez você tenha sacado que há um problema: Com o tempo, a busca degenera. Imagine que, se você sempre trata a colisão deslocando um elemento pra direita, a busca pode precisar checar todos os elementos seguintes até achar a chave pesquisada, ou mesmo simplesmente constatar que ela não está na tabela.

Pra evitar isso, precisamos garantir que o array não fique muito cheio, sempre mantendo o preenchimento abaixo de 50% aumentando o tamanho.

3.2.2 Hashing duplo

Uma segunda função hash, que encontra uma posição pra um elemento caso haja uma colisão. Há algumas regras que deixarei para atualizar depois. ……………….

4. Anotações para atualizações posteriores

• Há alguma variedade nas funções de dispersão? Se sim, qual?
• Colocar a função de busca utilizando encadeamento