Árvores heap (heap trees)

A heap é massinha por um motivo específico: Armazenando uma sequência de números nela, ela consegue sempre retornar o menor número (ou maior, se for uma maxheap) em tempo log(N).

1. Introdução

A árvore heap é uma forma de implementar o conceito de fila de prioridade. Note que na fila do banco existem duas prioridades: Especial (idosos, gestantes…) e comum. Já a nossa heap pode ter vários níveis.

2. Representação de prioridade

A prioridade de um nó na árvore heap é representada por um número: Se a prioridade são os números maiores, chamamos de min-heap (heap mínimo, menores primeiro). Já se a prioridade são os números menores, chamamos de max-heap (heap máximo).

Aqui irei considerar somente a min-heap, pois é o que Robinson usa.

3. Regras básicas (balanceamento)

Para uma heap ser considerada balanceada, há duas propriedades que ela precisa satisfazer para garantir seu funcionamento:

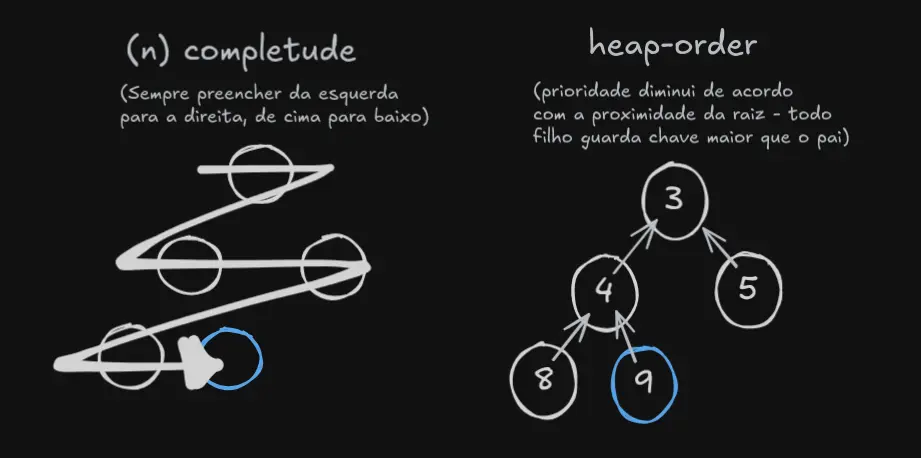
• Heap-order: Todo nó deve estar acima dos de menor prioridade
• Completude: a árvore deve ser preenchida da esquerda para a direita

4. Como inserir

Na inserção da heap, adicionamos o elemento num nó seguindo a propriedade de completude. A forma mais eficiente (O(logN)) de achar a posição de inserção é a seguinte:

Dentro do algoritmo para achar o próximo nó de inserção há dois casos. Veja bem, somente dois casos e pronto.

1. A árvore está completinha e você vai ter que achar o primeiro nó da última linha

2. A árvore está com a última linha incompleta e você vai precisar achar o irmão do nó que você está ou do de cima

O segundo passo é inserir o nó ali.

Depois, temos que subi-lo na árvore até ele estar na posição adequada.

E é isso.

4.1 Busca do local de inserção

A busca fica bem mais simples se a árvore guardar o último nó inserido. Vamos considerar que o nome desse atributo será lastNode.

A partir de lastNode, podemos fazer um caminho O(Log(N)) até o local da inserção, por meio das seguintes instruções:

• Subir até encontrar um filho esquerdo ou a raiz
• Caso encontre um filho esquerdo, ir para o filho direito e descer pela esquerda

Dessa forma, podemos inserir o elemento no lugar e tratar a posição dele depois.

4.2 Upheap

Já que colocamos o elemento no último lugar da árvore, precisamos subi-lo até uma posição coerente. Enquanto ele tiver maior prioridade em relação ao elemento de cima, trocamos os dois de lugar.

IMAGEM DOS ESTÁGIOS DA INSERÇÃO NA HEAP

5. Remoção

COMPLEXIDADES TEMPORAIS

Referências

Aulas e slides de Robinson

Aulas de Jorgiano